What is Calculus?
Primary tabs
Even if you never expect or need to take a course in Calculus, having a strong liberal education should include understanding some of the most basic concepts in science. The cornerstone of today's high tech, big data world is Calculus. It is the language and foundation of modern statistics, engineering, physics, chemistry, medicine, quantitative finance, and the list goes on. So if you have always felt that this subject was complicated then this article is here to answering in the simplest terms: What is Calculus?
Calculus comes in two flavors. The first is Differential Calculus and the second is Integral Calculus. Differential Calculus is finding the slope of curves (mathematicians call curves functions and denote them by $f(x)$) and Integral Calculus is finding the area under curves. Let's talk about Differential Calculus first.
Somewhere in high school you hopefully learned that the slope of a straight line is
\[
\mbox{Slope}=\frac{\mbox{Rise}}{\mbox{Run}}.
\]
Differential Calculus is about finding the slope of a function or curve that is not a straight line. We usually stop calling it a slope and start referring to it as a derivative and denote it by $f\,'(x)$ or $df/dx$. In other words,
\[
\mbox{Slope}=\mbox{Derivative}=f\,'(x)=\frac{df}{dx}.
\]
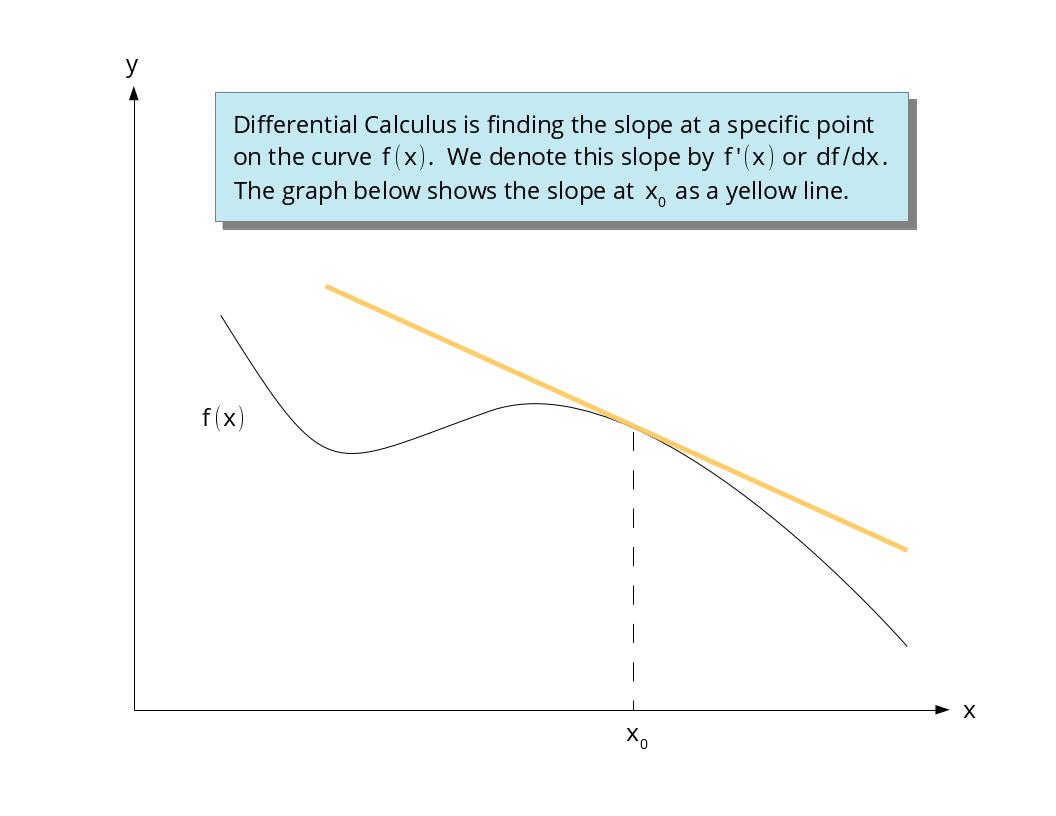
So let's explain why this gets complicated. To find the derivative (slope) in Calculus you have to determine the slope as both the rise and the run get smaller and smaller. In other words,
\[
\mbox{Derivative}=\frac{\mbox{Rise}\to 0}{\mbox{Run}\to 0}.
\]
If the rise approaches zero more quickly than the run, then the slope is zero. If the run approaches zero more quickly than the rise, then the slope becomes infinitely large. For most functions both the rise and the run approach zero in such a way as to produce some non-zero and non-infinite slope. How we do this is called function limits and is one of the first and most difficult concepts for beginning Calculus students.
Now let's explain Integral Calculus. When we were in Geometry class we had to learn the area of common shapes like rectangles, circles, squares, triangles, etc. In Integral Calculus we find the area underneath a curve. We refer to the area under a curve as an integral and denote it by
\[
\mbox{Integral}=\int\,f(x)dx.
\]
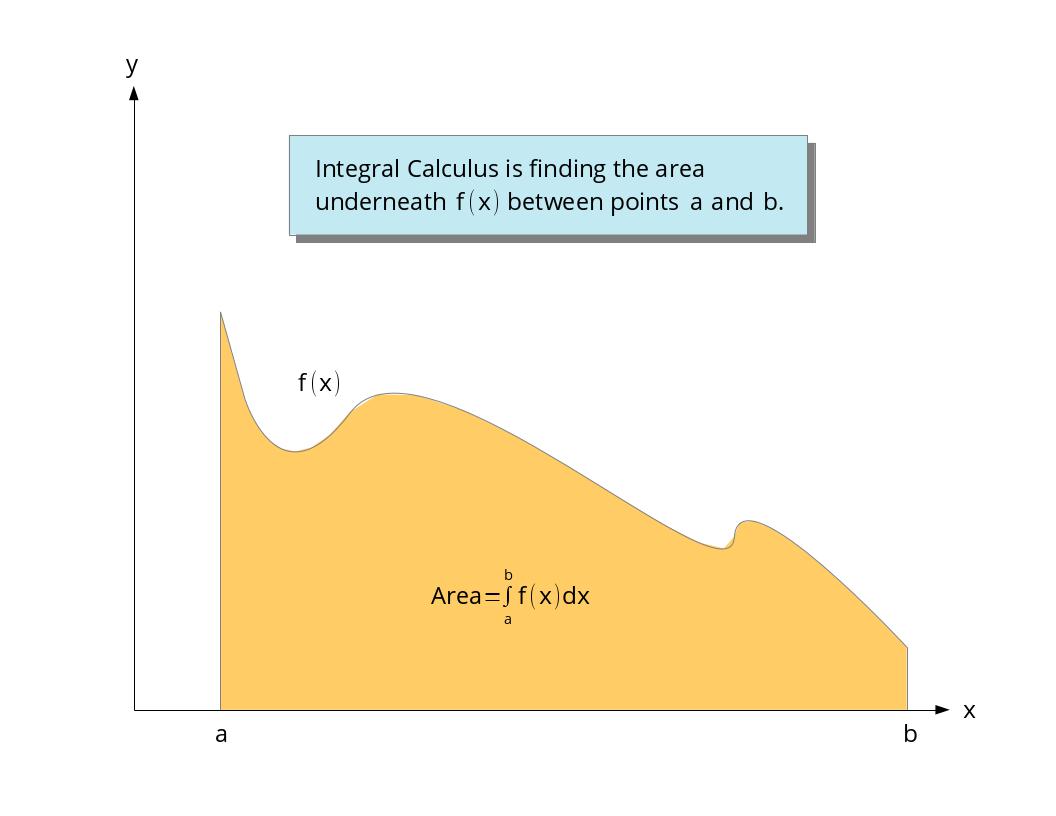
The way we do this in practice is to approximate the area under the curve by a bunch of rectangles. As we create rectangles of smaller and smaller width we need to have more and more of them to fill the area. In other words,
\[
\mbox{Integral}=\left(\mbox{Number of rectangles}\to\infty\right)\times\left(\mbox{Width of each rectangle}\to 0\right).
\]
As the number of rectangles becomes larger and larger the integral will become larger and larger. However, the rectangles have a smaller and smaller area because their width is getting smaller. The difficulty in Integral Calculus is figuring out whether the integral is infinite, zero or somewhere in between. For most of the functions that describe the real world, there is a sweet spot in this tug of war between infinity and zero that results in a real area that we can calculate.
Hopefully you now have a basic understanding of Calculus and don't need to take a class on it. However, if you do find yourself needing to know more, then we are here to help with lessons, problems and our function wizard to make learning Calculus easier.
