Arc Length
Primary tabs
One of the easiest and most important formulas in Mathematics is the formula for arc length. This simple formula has a lot of applications that we want to talk about in the future, but for now we want to explain what it is and how to calculate it.
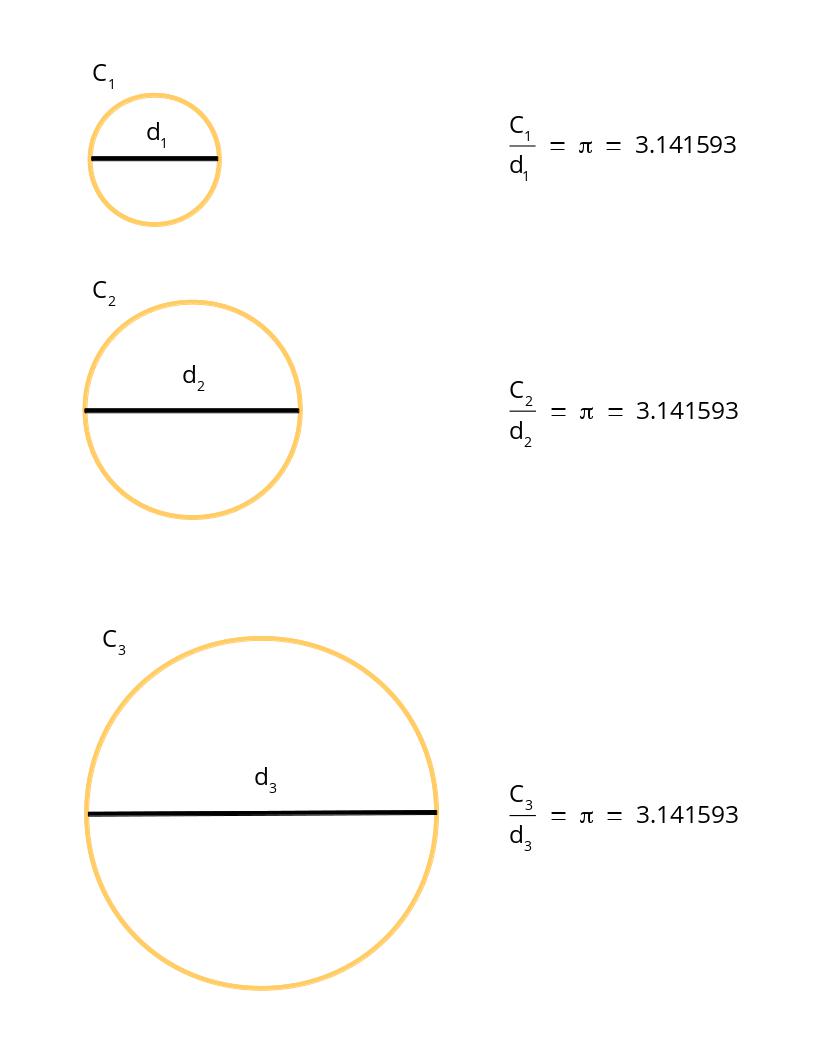
One of the first things we learned in school about Mathematics was that the ratio of the circumference of a circle (the length around a circle) to its diameter (the length across the circle) is the same no matter the size of the circle. This ratio is always the number $\pi$ which is equal to $3.141593$. In other words,
\[
\frac{C}{d}\,=\,\pi\,=\,3.141593.
\]
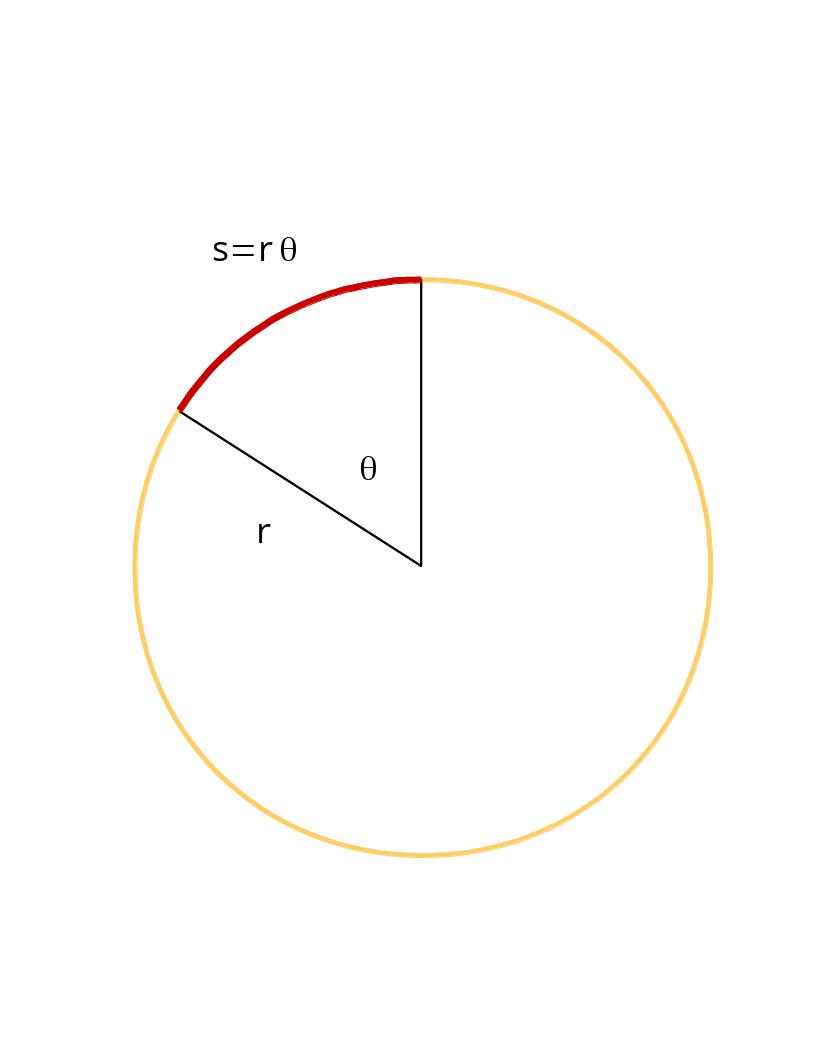
But how do we find the length of only part of the circumference? This is called arc length and has the formula
\[
s=r\theta
\]
where $s$ is the arc length, $r$ is the radius and $\theta$ is the angle measured in radians. In the picture below the arc length is in red.
We can immediately recover our circumference formula by putting in $\theta=2\pi$ to get $s=r\cdot 2\cdot\pi$. Since the diameter is $d=2r$ we get $s=d\cdot\pi$. Since we know that $C=d\cdot\pi$ we see that the $s$ is the circumference when $\theta=2\pi$.
To use this formula one must be aware of the units of the angle. We recently talked about units and dimensional analysis. For $s=r\theta$ to describe the real world its units on the left side of the equal sign must be equal to the units on the right side of the equal sign. This means that $\theta$ must not have a dimension - it can't be a length or any other unit. The number $\pi$ is a dimensionless quantity that is the angle half-way around a circle. We call the number $\pi$ (3.141593) the number of radians half-way around the circle. The number $2\pi$ is the number of radians around the circle. The formula $s=r\theta$ requires that we use radians and not degrees.
Most of the time we think in degrees. We know that a circle has $360$ degrees and we could be tempted to just stick the number of degrees $\theta$ is into $s=r\theta$. This is incorrect and we must first convert the number of degrees to radians. To do this let's assume that $\phi$ is our angle measured in degrees and $\theta$ is the same angle measured in radians. To convert to radians we use
\begin{eqnarray}
\theta&=&\left(\frac{2\pi}{360}\right)\,\phi\\
&=&\left(\frac{2\cdot 3.141593}{360\mbox{ degrees}}\right)\,\phi\\
&=&1.7453\times 10^{-2}\,\phi/\mbox{degrees}
\end{eqnarray}
Let's do a quick example. Let's say we want to find the arc length of part of a circle with a radius of $2$ feet and an angle of $30$ degrees. Since the angle is in degrees we must first convert it to radians. Following our formula above we have
\[
\theta=1.7453\times 10^{-2}\,\cdot 30\mbox{ degrees}/\mbox{degrees}=0.52359
\]
(Notice how the degrees cancel to give a dimensionless quantity for the angle.) Now we can find that our arc length is
\begin{eqnarray}
s&=&r\theta\\
&=&2\mbox{ feet}\cdot 0.52359\\
&=&1.04718\mbox{ feet}.
\end{eqnarray}
That's it! This formula is very easy with the only thing we need to be aware of is the units of the angle. Making sure the angle is converted to radians is the only difficult part in finding an arc length.
