Calculus Rhapsody - The Math Behind This Creative Video You're Guaranteed to Be Tested On

If you haven't seen it, the Calculus Rhapsody music video on Youtube is worth watching. It's creative, funny, and educational all at the same time. So what does this video teach us? Did they get anything wrong? What did they get right? Let's go through the video to see what parts of Calculus they're singing about.

First, here's the video:

At the very beginning they ask, "Is this \(x\) defined?" What they probably mean is, "Is this \(f(x)\) defined?". The variable \(x\) is typically used to denote a real number. For example, \(x=2\). The \(x\)-axis is the set of all real numbers, and the domain of a function is where on the \(x\)-axis the function is defined. A function may or may not be defined for certain values of \(x\). For example, if we know that \(f(2)=17\), then the function is defined at \(x=2\). If we don't know the value of \(f(x)\) at \(x=2\), then the function is undefined there. So the correct way to think about it is "where on the \(x\)-axis is \(f(x)\) defined" and not "is this \(x\) defined."

Calculus rhapsody quickly moves into important limit concepts you need to know

Next they say: "Is f continuous? How do you find out? You can use the limit process." This is absolutely correct! To understand what they're talking about you first have to know what a function limit is. It's denoted by

\[\lim_{x\to a}f(x)=L\]

and it means that as \(x\) gets closer and closer to \(a\), then the function get closer and closer to \(L\).

But there's something important that you need to understand here. You see, a function can have a different value at \(a\) than what its function limit is at \(a\).

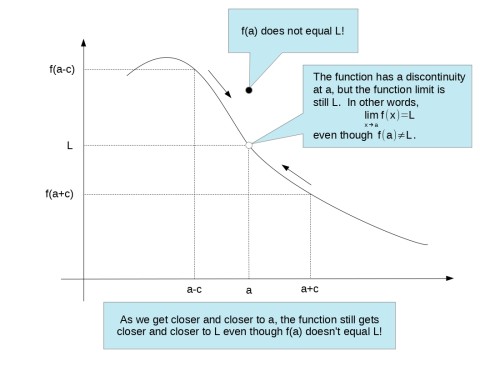
So the value of the function at \(a\) and it's function limit at \(a\) can be the same number or two different numbers. When they're the same, the function is said to be continuous at that point.

A practical and down-to-earth definition of continuity is that when you draw the function you don't have to pick up your pencil to put it on anther spot. If the function isn't continuous, you'd have to pick your pencil off of the paper and put a dot where the value of the function is at that discontinuous spot as the image above suggests.

So they absolutely got this right. Continuity is defined as \[\lim_{x\to a}f(x)=f(a).\]

Next they say "Approach from both sides. The left and the right meet." This really points out that a limit is defined if the left-sided limit equals the right-sided limit.

Another way to think of it is this way. What if the limit from the left didn't equal the limit from the right? Check out the picture below.

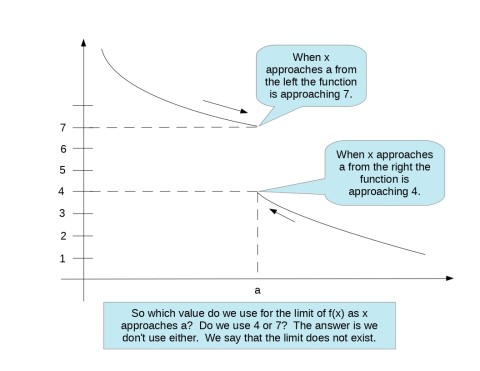
When the limit from the left doesn't equal the limit from the left we say that the limit is undefined or does not exist. So they're absolutely correct on this point.

"I'm just a limit, defined analytically" True, but what do they mean by this? When we say something is defined analytically we really mean that it has a formal, logical definition. You can check out the analytical definition here.

"Function's continuous, there's no holes, no sharp points, or asymptotes" This is not fully correct. It's true that a continuous function will not have holes or asymptotes, but it is NOT true there there will be no sharp points. A continuous function can have sharp points. The simplest example is that of the absolute value function which has a sharp point at \(x=0\). It's also continuous there as the formal limit definition shows.

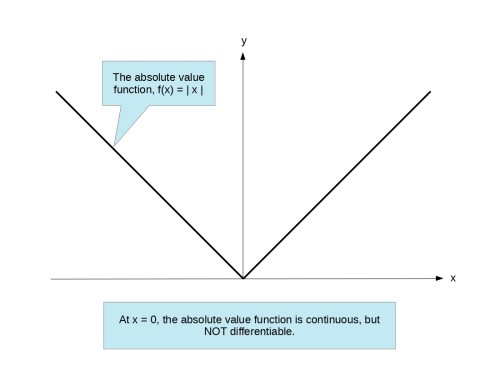
"Anyway this graph goes, it is differentiable to me." Be careful. I know there is some artistic license going on here, but you can't always differentiate a function. More specifically, a derivative is defined at a specific point and may or may not exist at that point. Let's use the absolute value function again. It is not differentiable at \(x=0\), but it's differentiable everywhere else.

Calculus rhapsody highlights four derivative rules you will be tested on: power rule, product rule, quotient rule, and chain rule

"\(y\)-prime . . . oooh . . . . is the derivative of \(y\)." This is true as \(y\,'\) is how you can denote the derivative of a function. It's more appropriate to say \(f\,'(x)\), but they get it.

"y equal x to the n, dy/dx equals n times x to the n-1." This is true. Remember that we can denote the derivative by \(y\,'\) or by \(dy/dx\). This second method is the Liebniz notation. If \(y=x^n\), then \(y\,'=nx^{n-1}\). This is just a statement of the power rule. The power rule is one of the first four derivatives you must learn.

"Other applications of derivatives apply if y is divided or multiplied. You use the quotient and product rules." This is important. When you want to find the derivative of a function that's made up of two functions multiplied by each other, you use the product rule which states that \[\frac{d}{dx}\big(fg\big) = \frac{df}{dx}g+f\frac{dg}{dx}.\] And if a function is made up of two functions divided by each other you use the quotient rule which says that \[\frac{d}{dx}\Bigg(\frac{f}{g}\Bigg) = \frac{1}{g^2}\Bigg(g\frac{df}{dx}-f\frac{dg}{dx}\Bigg).\]

The product rule is easy to remember, but the quotient rule is harder to keep in your head. I have an easy way to remember the quotient rule in my book Calculus in 5 Hours which you can get here.

"Also . . . oooh . . . don't forget to do the chain rule. Before you are done you gotta remember to multiply by the chain." The chain rule states that \[(f\circ g)\,'(x)=f\,'(g(x))g\,'(x),\] or in Liebniz notation it's \[\frac{d}{dx}f\circ g = \frac{df}{dg}\cdot\frac{dg}{dx}.\] So are they saying that you need to remember to multiply by the \(g\,'(x)\) at the end? Probably.

Next, they head into integrals, antiderivatives, and the Fundamental Theorem of Integral Calculus

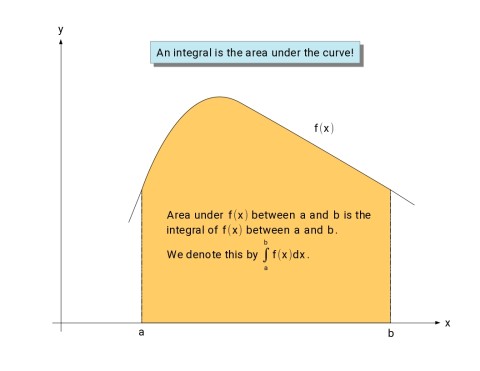
"I need to find the area under a curve. Integrate! Integrate! You can use the integration." Yes, integration is the area under a curve.

"Raise exponent by one, multiply the reciprocal." Here they're finding the antiderivative of \(x^n\) which is \[\frac{x^{n+1}}{(n+1)}.\] So to find the antiderivative you add 1 to \(n\) and then multiple \(x^{n+1}\) by \(1/n+1\). The ntiderivative is used to find the value of the integral from the Fundamental Theorem of Integral Calculus which is what they are doing in the next line they sing.

Then the say "Add a constant. Add a constant. Add a constant. Add a constant. Add a constant labeled \(C\)." This is the constant of integration and the fact that they are saying this is telling us that they're doing an indefinite integral as opposed to a definite integral. So to summarize, they're saying \[\int x^n\,dx=\frac{1}{n+1}x^{n+1}+C.\]

A final barrage of advanced Calculus topics

"Can you find the area between \(f\) and \(g\)? Integrate \(f\) and then integrate \(g\). Then subtract." This is correct. To find the area between \(f(x)\) and \(g(x)\) you do the following: \[\int_a^b f(x)\,dx-\int_a^b g(x)\,dx.\]

Next they say "To revolve around the \(y\)-axis integrate outer radius squared minus inner radius squared multiplied by pi . . . multiply the integral by pi . . ." Here they're finding the volume between two functions by spinning the two functions around the \(y\)-axis.

To do this you first find \(x\) as a function of \(y\). So instead of having \(y=f(x)\) you solve for \(x\) to get \(x=F(y)\), and you do the same thing for \(y=g(x)\) to get \(x=G(y)\). Once you do that your volume will be \[V=\pi\,\int_a^b[F(y)]^2-[G(y)]^2\,dy.\] Go to this Wikipedia article for more info on this technique.

Then they throw this in: Pre-calculus did not help me to prepare for Calculus, for Calculus, help me! Most student feel this way and it's true. Calculus requires a different way of thinking and there's really nothing that can fully prepare you for that. But don't worry, you can still understand it and do well.

"So you think you can find the limit of y . . . so you think you'll find zero and have it defined . . . oh, baby, you can't define that point baby" is probably a reference to the picture in the video of the function \(1/x\) which is not defined at \(x=0\). This is a good reference for them to make. A function limit can exist at a point where a function is not defined. Remember that the function limit is what the function "intends" to be and not what it is at that point.

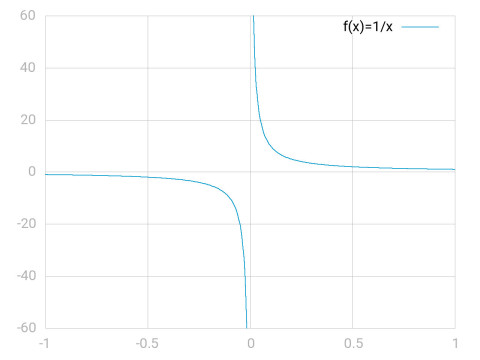
But some functions may have may have points on the \(x\)-axis where they aren't defined and they're function limits aren't defined there either. This is the case for \(1/x\) at \(x=0\). The function is not defined at \(x=0\) because you can't divide a number by zero.

At the same time, it's function limit is not defined at \(x=0\) for two important reasons. First the function goes to infinity - meaning that it is unbounded at \(x=0\). Second, even if it were bounded, it's taking on both negative and positive values at \(x=0\). This means the left-sided and right-sided limits would not be equal and the function limit would not exist. (Remember for a function limit to exist its left-sided and right-sided limits must equal.)

Of course the song continues on to say "it's undefined, goes to positive and negative infinity" which is what I was saying - only they say it better!

Finally, this video follows the progression of a typical Calculus course. You'll learn about function limits first followed by derivatives, rules for calculating derivatives, antiderivatives, and then integrals.

So now that you know the Calculus they're singing about, go back through the video to reinforce your understanding of the concepts. This entertaining video has a lot of Calculus in it. If you understand what they're talking about you'll do well in your class.

Great job, guys, on your Calculus Rhapsody video. I hope you both got an A!