Integrating Functions with Sage!

Primary tabs

This is the fourth lesson in five where we are discussing Sage and how it can be used to make your Calculus life easier. In the first lesson you learned how to create your own account and how to create a worksheet. In the second lesson you learned how to plot functions with Sage. In the third lesson you learned how to differentiate using Sage. In this lesson we are going to learn how to calculate integrals. So to get started log into your account, create a new worksheet and label it integrals. You can do this by clicking the "New" button, typing "integrals" in the text box and hitting the "Sage Worksheet" button just as we did in the first lesson.

Now you should have a worksheet where you can type in commands. We are going to use sage to solve
\[
\int_0^1x^3+3x^2-8x-2\,dx.
\]
The full solution is here and we know that the answer is -19/4. Let's solve this with Sage. First, input the function as we did yesterday like so:

To solve the indefinite integral of this function we need to use the command "f.integral(x)" like this:

Solving an indefinite integral with Sage

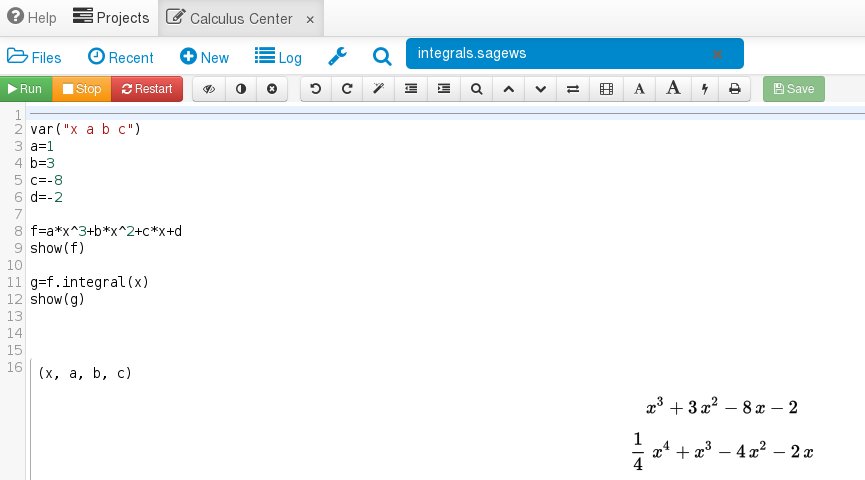
To solve the definite integral we use the command "f.integral(x,0,1)". The lower and upper limits of integration come right after the x. This is what we get:

Solving a definite integral with Sage

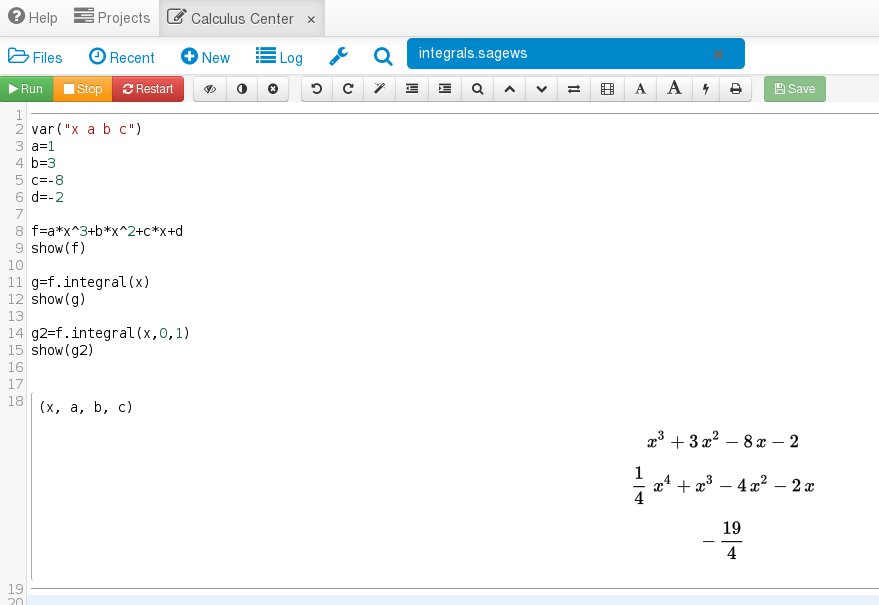
Finally, using our plotting skills let's visualize the area we are finding with the following code:

Plotting the definite integral with Sage
What we have done is use the fill=True parameter in our plot command to shade in the area we are integrating. To show the function outside of that area we have a second plot that goes beyond our limits of integration.

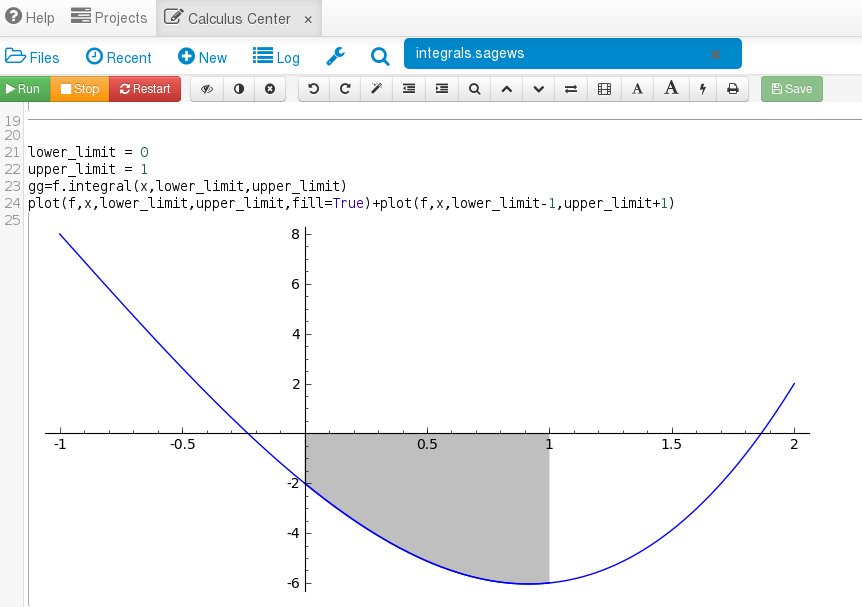
To summarize, in Sage we solve both indefinite and definite integrals this way:
\begin{eqnarray}
\mbox{f.integral(x)}&=&\int\,f(x)dx\\
\mbox{f.integral(x,a,b)}&=&\int_a^b\, f(x)dx.
\end{eqnarray}

Tomorrow we will use Sage to find critical points and functions limits. Finally, if you want to jump to the other blog posts for Sage Week then here they are: