Finding Critical Points and Limits with Sage!
Primary tabs
This is the fifth lesson in five where we are discussing Sage and how it can be used to make your Calculus life easier. In the first lesson you learned how to create your own account and how to create a worksheet. In the second lesson you learned how to plot functions with Sage. In the third lesson you learned how to differentiate using Sage. And in the fourth lesson you learned how to integrate functions with Sage. In this lesson we are going to show how you can find critical points and solve limits. So to get started log into your account, create a new worksheet and label it 'critical points and limits'. You can do this by clicking the "New" button, typing "critical points and limits" in the text box and hitting the "Sage Worksheet" button just as we did in the first lesson.
First, let's introduce the solve function by solving a quadratic equation. Create a polynomial as you have done in the other lessons and then type the command "g=solve(f==0,x)" and then "show(g)". Like this:
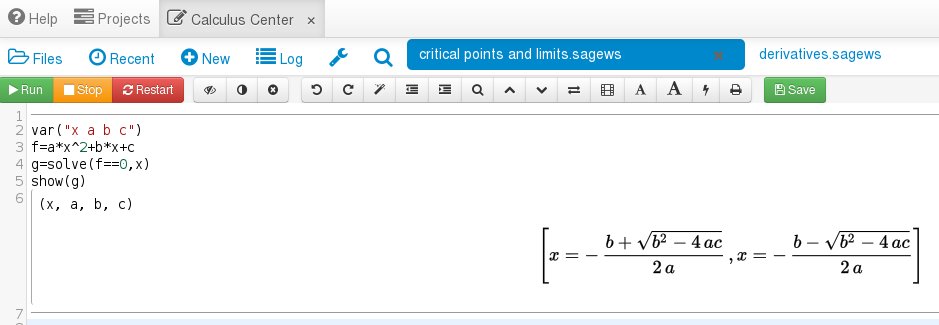
Recall that critical points are where a function's derivative is zero or is not defined. So let's find those points where the derivative is zero using the solve function:
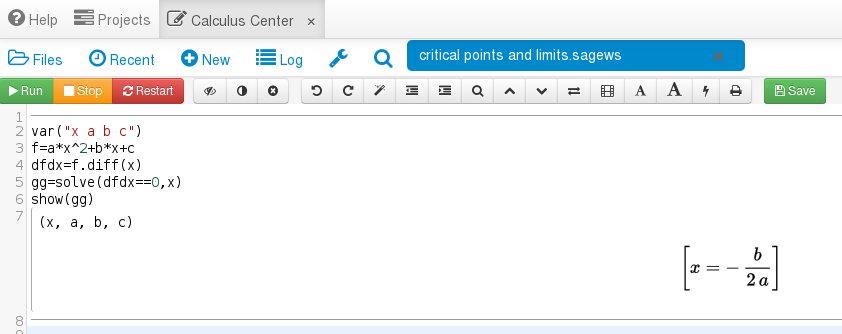
\begin{eqnarray}
f(x)&=&ax^2+bx+c,\\
\frac{df}{dx}&=&2ax+b=0,\\
x&=&-\frac{b}{2a}.
\end{eqnarray}
Be careful! This only works for functions that are polynomials. For functions like $1/x$ you will have to do other things like solve(f==oo,x) to solve it. A full discussion of critical points is beyond the scope of today's discussion so we will have to save it for later. Let's move to limits.
Let's solve
\[
\lim_{x\to 2}\,\frac{5x^2-3x-14}{x-2}.
\]
We know from here that the answer is 17. To do this we use the limit command like so:
![\[ \lim_{x\to 2}\,\frac{5x^2-3x-14}{x-2}. \] Solving limits with Sage](/sites/default/files/field/image/sage_article_critical_points_and_limits_3.jpeg)
We hope that you enjoyed Sage Week. You can find more Calculus information on the Sage Calculus Tutorial page. Finally, if you want to jump to the other blog posts for Sage Week then here they are:
- Monday: Make your Calculus life easier with Sage!
- Tuesday: Plotting functions with Sage!
- Wednesday: Differentiating functions with Sage!
- Thursday: Integrating Functions with Sage!
- Friday/Today: Finding Critical Points and Limits with Sage!
