Exponentially Increasing Function

Have you ever wondered what it means to have something increase exponentially? When someone says this they usually mean really fast or really big. We want to tell you what this means and to show you in pictures why something that increases exponentially increases a lot and very quickly.

Calculus deals with functions. A function is where we put in a value for $x$ and get only one value for $y$ back. We typically graph this with the "x-axis" going horizontally and the "y-axis" going vertically. We typically call our function $f(x)$. Our image below is of an arbitrary function that we made up.

For example, a straight line would be $y=x$ or more formally $f(x)=x$. Another example would be $f(x)=2x$. The function will take a value for $x$ and give back two times $x$. If $x=3$ then $y=6$.

Two very important functions in Calculus are the exponential function and the logarithm function. The exponential function is denoted by $f(x)=e^x$ or sometimes by $f(x)=\exp(x)$ where $e$ is the number $2.7183...$. The logarithm function is denoted by $f(x)=\ln(x)$.

These two function are actually related. If we put one in the other through a mathematical process called function composition we see that
\[
\ln(\exp(x))=x
\]
and
\[
\exp(\ln(x))=x.
\]
When this relationship holds we say that they are inverses of each other.

So let's finally get to the point. We are going to graph $y=\exp(x)$, $y=x$, and $y=\ln(x)$. Here they are:

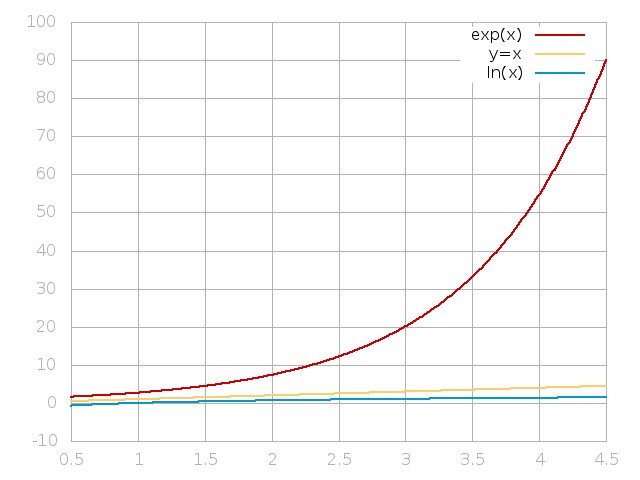
Wow! Look at that exponential function go! As $x$ gets bigger and bigger all three functions will get bigger and bigger. In fact we say that they go to infinity. But the exponential function will approach infinity much more quickly. So this is why when someone says something increases exponentially they really do mean really big or getting big very fast. Conversely, if we said that something increased logarithmically then we would mean that it gets big, but only very slowly.

Here at CalculusSolution.com we want your understanding of Calculus to grow exponentially. We can help with lessons, problems and our function wizard to make learning Calculus easier.